Exponential Explorations – Part I
During my visit at the home of Mrs. Balabusta and Psychotoddler, I had the pleasure of meeting Gerald Glazer, a retired math professor. It’s not every weekend that I meet someone with as much interest in recreational math as me (or more!) so it was quite a treat to work on the math puzzles he tossed at me while dining on Mrs. B’s yummy cuisine.

One of the problems he gave me had me thinking for quite a while and even after solving it, led to some interesting discoveries. Allow me to give you the puzzle first, and then after one of you solves it, we’ll explore a little further in Part II.

Here’s the problem.

Define f(x) as follows.

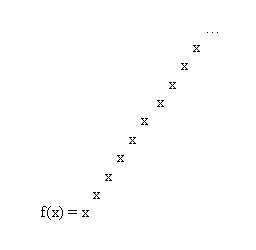
Where the dot dot dot at the top means keep going with the ladder of exponents forever.

Find x such that f(x) = 2. Show your work.

Now, let me make sure you don’t make the mistake I made when I first heard this problem. I got the order of the exponentiation backwards. I initially thought that the function was (((x^x)^x)^x)… Meaning, if we were to plug in 1.2 for x we would calculate 1.2 to the 1.2 power, to the 1.2 power, to the 1.2 power, and so on. That’s NOT right. Since (a^b)^c = a^(bc) that would have meant that f(x)=x^(x x x x…) which for any x > 1 is infinite.

The right way to read the function is f(x) = …x^(x^(x^(x^x))). That means you first start with the top exponent and work your way down the ladder. Meaning, if we were to plug in 1.2 for x the way to calculate it is 1.2 to the 1.2 power. Then 1.2 to that power, then 1.2 to that power, and so on and so on forever. Makes sense?

So find x such that plugging it into that function results in 2. - served up by Doctor Bean @ 7:42 PM